Monday, January 27, 2014
Temperature hiatus update
by
eduardo
The data of the
global annual mean near-surface air temperature of three data sets,
HadCRUT4, GISSTEMP and NCDC is now out for the whole 2013. It is thus
time for a brief update about
the status of the recent temperature hiatus.
The global mean
temperature was on average in 2013 0.02 K warmer than 2012 according
to HadCRUT4, 0.03 C warmer according to GISTEMP and 0.05 C
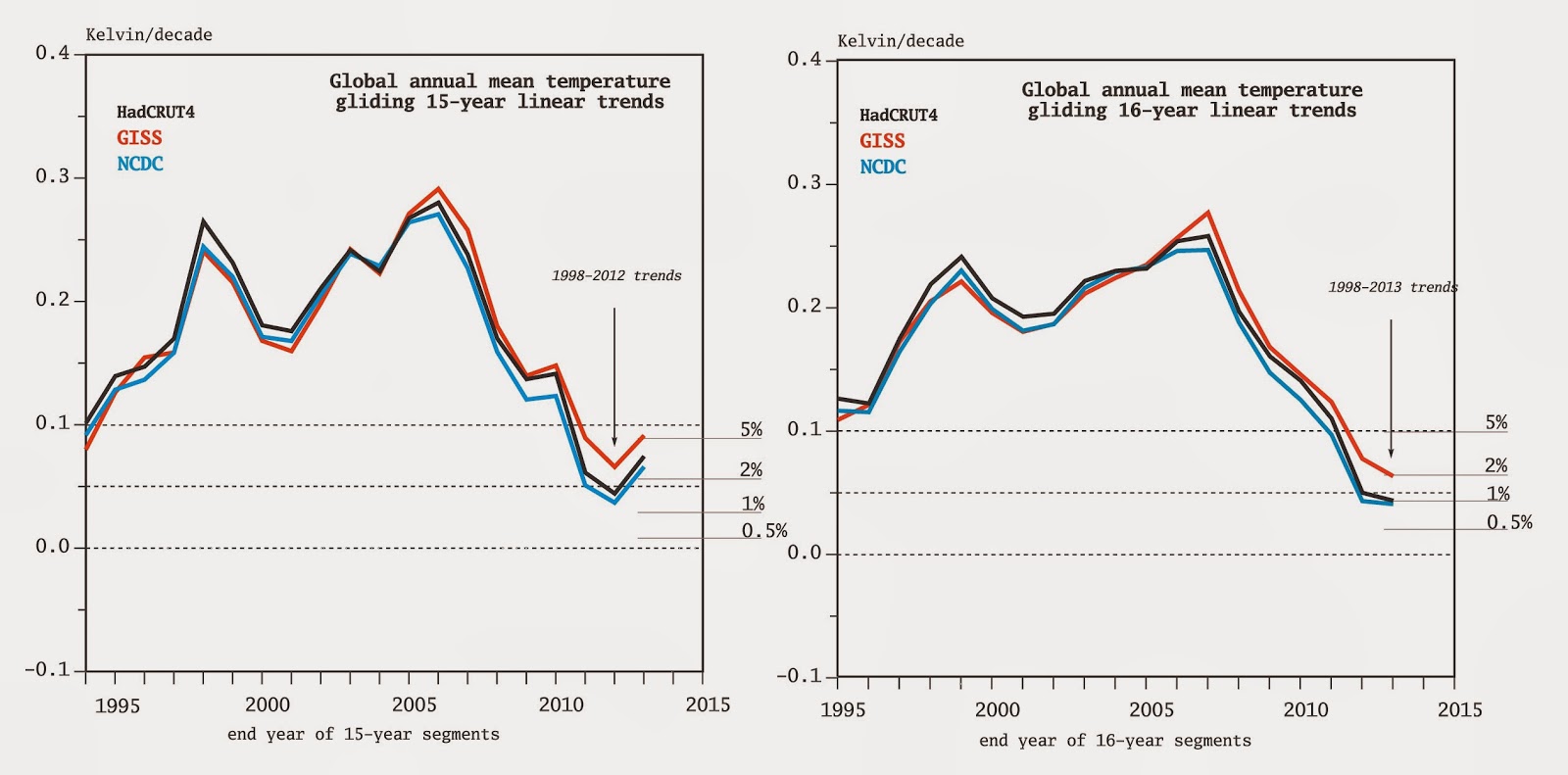
according to NCDC. The central estimates of the 15-year 1999-2013
trends were 0.074 C/decade , 0.093 C/decade and 0.066 C/decade for
HadCRUT4, GISSTEMP and NCDC (compared to the 1998-2012 trends of
0.042 C/decade, 0.063 C/decade and 0.037 C/decade), and the 16 years
trends since 1998 of 0.043 C/decade, 0.064 C/decade and 0.0410
C/decade, respectively.
With one more data
point, an update of the recent temperature trends of the last 15
years can be constructed in two ways: by computing the trend over the
now last 15 years (1999-2013) or by including the last year (2013) in
the previous 15-year segment, yielding a 16-year segment. The
difference is important because we would like to test whether or not
the temperature trends are compatible with the IPCC model ensemble.
In our last assessment we used all 15-year temperature trends
produced by the IPCC models driven by scenario RCP4.5 over the period
2005-2060. Over this period the external forcing is very close to
linear and the ensemble of all 15-year trends should encompass the
expected trend due to the external forcing plus the spread caused by
internal model variability plus the inter-model structural
uncertainty. The total spread should thus represent the total
uncertainty, from the models point of view, of the 15-year trend.
The spread depends on the length of the time segment. Longer segments
yield narrower modelled spreads of temperature trends , as these
trends are become increasing dominated by the deterministic external
forcing and decreasingly affected by internal and inter-model
variability. This is why the agreement between modelled and observe
trends should increase with longer time segments.
The results of
both types of update are summarized below. In brief, the hiatus is
still with us. Considering now the 16-year trends, the observed
trends have been become even less compatible with the model spread
than they were before.
In the left panel
we have displayed the gliding 15-year temperature trends derived from
the three data sets. The trends in the period 1999-2013 are somewhat
higher than the 1998-2012 trends. This reflect both that 2013 has a
bit a bit warmer than 2012 but also that the warm year 1998 is now
not included the in the last 15-year segment 1999-2013. The compatibility with the 15-year trends produced by the IPCC models
(here, only CMIP5 have been considered) has marginally increased. For
instance, whereas less than 2% of all model trends lied below the
HadCRUT4 trend for 1998-2012, this percentage is now 3%.
Comparing the
observed and modelled 16-year trends (right panel), the observed
trend in the last 16 year period is smaller, in all data sets, that
the previous 16-year segment. For this segment length, therefore, the
observed trend differs more clearly from the model ensemble. Since
the ensemble of trends for 16-year segments gets narrower, the
compatibility between observed and model trends for 16-year segments
has worsened: about 1% of the model trends are as small or smaller
than the observed HadCRUT4 and NCDC trends in 1998-2013, and about 2%
of the model trends are below the GISS trend in 1998-2013.
A look at the
temperatures of the lower-troposphere derived from satellite data is
also instructive (see figure below for trends derived from the
monthly means, not annual means). Both trends, near-surface and lower
troposphere, are predicted by models to be different, the
lower-troposphere trends caused by the external forcing should be
warmer than at the surface. There are two 'competing' satellite data
sets, one from the University of Alabama in Huntsville and another one from Remote
Sensing Systems. Although both groups used the same raw satellite data, the
corrections applied to take into account satellite drifts and to
stitch together different satellite missions are different. Thus the
final result also differ. What is quite remarkable here is that the
trends computed from the RSS data become even negative and clearly
differ from the UAH trends, illustrating the quite large
uncertainties that still exist. For the satellite data, the
comparison with the modelled trends is not as straight forward, since
the satellite-derived temperatures represent a weighted averaged over
several tropospheric layers and not directly the temperature at a prescribed height
Subscribe to:
Post Comments (Atom)






48 comments:
Ich gebe zu, ich weiß einfach immer noch nicht, welche Schlüsse ich aus der ersten Abbildung ziehen soll.
Ja, ich sehe, dass solche 15-Jahrestrends wie die gegenwärtigen in den Modellensembles selten vorkommen. Aber welche Schlüsse kann ich daraus ziehen?
Es gibt ja zwei Möglichkeiten:
a) Die Modelle passen nicht richtig, weil die gegenwärtige Phase eben nicht besonders "unnormal" ist, damit ist das Auftauchen solch niedriger Trends dubios.
b) Die Modelle passen ganz gut und geben korrekt wieder, dass wir uns gegenwärtig in einer sehr außergewöhnlichen Phase befinden.
Kurz: Um die Ergebnisse bewerten zu können, müsste ich wissen, wie selten, wie ungewöhnlich die gegenwärtige Phase im realen Klimaverlauf ist.
Bei welchem Wert würden Sie, Eduardo, mit den Ergebnissen zufrieden sein? Bei 5%, 10% oder vielleicht sogar 20%? Was ist der Referenzwert, an dem ich mich orientieren kann?
Ich habe das Gefühl, dass man mit dieser hier dargestellten Methode nicht wirklich einen Fortschritt erreichen kann. Reine Statistik hilft wohl nicht weiter, wir müssen uns wohl konkret um die Aufklärung der beteiligten Mechanismen kümmern.
Und ich stelle fest, dass Statistik trügerisch sein kann: Ist es nicht bemerkenswert, wie das unspektakuläre Jahr 2013 die Trendwerte deutlich verändert hat? Man merkt, welchen Einfluss der El-Nino-Ausreißer auf den Trend hat, wenn der Ausreißer am Rand des Intervalls liegt.
Berücksichtig man Cowtan und Way, dann könnten die Trendwerte noch etwas höher liegen.
Wie gut passt die Entwicklung des Forcings in den letzten 10-20 Jahren zum linearen Forcing bis 2060? Schwächelnde Sonne, enorme Unsicherheiten bei den Aerosolen.
Alles, was ich mit diesen Beispielen ausdrücken will, ist: die Prozentzahlen in Abbildung 1 könnten möglicherweise auch etwas höher sein. Ab welchem Wert wären wir denn zufrieden mit unseren Modellen?
Viele Grüße
Andreas
Was heisst hier 'passen' ? zu was passen ?
Die Abbildung zeigt einen Hypothesen-Test (obwohl strikt gesehen, die Ausführung dieses Tests sollte etwas komplizierter sein)
Die Hypothese lautet: der beobachtete Trend 1998-2012 ist das Ergebnis des externen GHG Forcing + eine Realisation der stochastischen internen Variabilität, und zwar so wie von den Modelleden produziert.
Um diesen Test auszuführen, rechnen wir eine Verteilung der Trends mit GHG + interne Variabilität, und zwar so wie von den Klimamodellen erzeugt wird.
Man sieht, dass nur 2% dieser Trends so klein oder kleiner als der Beobachtete Trend ist. Die Schlussfolgerung würde lauten, dass die Hypothese, bei einem Signifikanzniveau von 98%, falsch ist. Das könnte drei Ursachen haben:
-die extern, von GHG,angetrieben simulierten Temperaturtrends falsch sind
-dass die von den Modellen erzeugte interne Variabilität zu klein ist
- außer GHG gibt es andere Forcings
Wie bei jedem Test, akzeptiert man hier ein Risiko von 2% , die Anfangshypothese fälschlich abgelehnt zu haben. Mit anderen Worten, es könnte doch noch sein, dass die Anfangshypothese richtig ist, man hätte nur per Zufall ein seltenes Ereignis erwischt.
'
Bei welchem Wert würden Sie, Eduardo, mit den Ergebnissen zufrieden sein? Bei 5%, 10% oder vielleicht sogar
20%? Was ist der Referenzwert, an dem ich mich orientieren kann?
'
Was heisst hier zufrieden ? ich bin weder zufrieden noch unzufrieden. Es ist dem einzelnen überlassen, mit welchen Signifikanzniveau jeder einzelne die Hypothese als widerlegt betrachtet.
Wenn ich mein Auto zur Werkstatt fahre, um die Bremsen zu testen, und die Werkstatt mir sagt, dass die Bremswirkung unter 80% aller 'normalen' Werte gelegen hat, habe ich 2 Optionen:
-das Messgerät hatte gerade hatte einen schlechten Tag gehabt, weiter fahren wie bisher.
- irgendwas ist nicht in Ordnung.
Ob man der Schlussfolgerung 'irgendwas ist nicht in Ordnung' bei 80%, 85%, 90%, oder 99% folgt, ist eine persönliche Entscheidung,
Eduardo,
irgendwie will es nicht in meinen Kopf hinein, bin ja auch kein Statistiker.
Ja, Hypothesentest. Mir geht ein (analoges?) Beispiel durch den Kopf:
Ich simulieren Wurfserien eines fairen Würfels. Mit dem Modell eines fairen Würfels berechne ich eine Verteilung, wie häufig Einsen in einer Wurfserie von 3 Würfen vorkommen.
Nun nehme ich einen realen Würfel und würfle einfach mal drauflos. Ich finde eine Folge von 3x die Eins nacheinander, picke diese Folge heraus, und führe einen Hypothesentest durch.
Ergebnis:
3x nacheinander die Eins ist ein überaus seltenes Ereignis, mein Modell des fairen Würfels ist fragwürdig.
Nun habe ich es geschafft, mich selbst hereinzulegen. Der Grund ist, dass ich nicht eine zufällige Abfolge dreier Werte ausgewählt habe, sondern eine Abfolge, von der ich schon vorher wusste, dass diese sehr selten ist.
Es ist genau dieses Beispiel, was mich verwirrt.
Übertragen auf die Temperaturtrends:
Wenn man diese Art von Hypothesentests macht, müsste man nicht besser per Zufallsgenerator einen beliebigen 15-Jahres-Zeitraum auswählen?
Und wenn ich schon einen der letzten 15-Jahrestrends nehme, müsste man dann nicht mit Bayes arbeiten? Etwa in der Art: Wie groß ist die Wahrscheinlichkeit, dass die Modelle diesen niedrigen Trend reproduzieren unter der Voraussetzung, dass in diesem Zeitraum auch die Modelle von einem negativen ENSO-Trend ausgehen (oder so ähnlich)?
Ich vermute mal, irgendetwas stimmt an meiner Würfel-Analogie nicht. Aber was?
Viele Grüße
Andreas
We have hear a situation where the test has been formulated when the data is already known. That must be taken into account in interpreting the results. Standard rules for deciding the significance of the observation that only 2% of the model runs produce a rate of temperature change larger or equal to the observed do not apply. At the minimum the hypothesis should be formulated to include deviations in both direction from the average model prediction: 4% of model runs deviate as much from the average.
Even that is not fully satisfactory. Statistics does not provide any clear rules for testing the significance of an observation that's used in formulating the test.
@Dr. Zorita
1998 war ja ein Extrempunkt. Werner Krauss sagte mal: der kommt immer zweimal. Finde ich auch: am Ende und am Anfang eines Zeitraums zur Trendberechnung.
Meine Fragen:
Wie verhalten sich eigentlich die Modelle nach einem extremen El Nino? Gibt es in den Modellläufen solche Punkte? Ist eine solche Untersuchung sinnvoll?
Es gab mal Modellexperimente, in denen das Arktiseis entfernt wurde und dann getestet wurde, was dann im Modell passiert.
Gruß,
EinAnonymerMitleser
Eduardo und Andreas,
Ich sehe das so wie Andreas. Kurioserweise hat ein Hans von Storch auf diesen (wie mir scheint) beliebten Fehler in seinem Statistik-Lehrbuch (6.4.1, "Mexican Hat") aufmerksam gemacht.
Da nun derselbe Mann das vorliegende Argument unterschreibt und bisher nicht durch gröbere Diskontinuitäten im Denken aufgefallen ist, liegt das Problem wohl bei mir.
Hilfe.
Vielleicht wäre es hilfreich, den Test weiter formal aufzudröseln.
1. Was ist die Zufallsvariable? a) Ein 15y-Trend (zufällig aus einer Klimarealisation gezogen), oder b) eine Klimarealisation (und die Frequenz der 0-Trends ist Teil der Teststatistik)?
Falls a), ist das kompatibel mit der durch die Überlappung induzierten Abhängigkeit der Trends?
2. Was ist die Teststatistik? gleich der ZV (1.a)? Die Frequenz von 15-jährigen 0-Trends? Die Anzahl der 15-jährigen 0-Trends in einem 56-Jahre Abschnitt?
Wie lautet die Beschreibung des "Experiments", das zur Beobachtung ("1 15y-0-Trend in den Obsdaten von 1957 bis 2012" oder etwas anderes?) geführt hat?
@Eduardo
"Wenn ich mein Auto zur Werkstatt fahre, um die Bremsen zu testen, und die Werkstatt mir sagt, dass die Bremswirkung unter 80% aller 'normalen' Werte gelegen hat, habe ich 2 Optionen: "
Da laeuft man schnell in das Problem der bedingten Wahrscheinlichkeiten. Die Wahrscheinlichkeit tatsaechlich ein Problem mit edn Bremsen zu haben, waere selbst bei nur 0.1% falschen Tests immer noch verschwindend gering (wenn die apriori Wahrscheinlichkeit kaputter Bremsen bei zb 0.001% laege).
Von 88 bis 98 (vielleicht kann man das Intervall noch optimieren) war die Erwaermung sehr stark. Kannst du leicht ausrechnen, was die Wahrscheinlichkeit ist, dass diese starke Erwaermung noch innerhalb der Modelbandbreite bei ausschliesslichem GHG Forcing liegt?
Georg
@ hvv,
' liegt das Problem wohl bei mir.#
Enverstanden, weil the Mexihat hat-paradox findet hier keine Anwendung.
In the Mexican-hat paradox, the distribution under the null.hypothesis is constructed from the very same data that were used to formulate it: For instance, I am in a forest and see one red tree among 1000 greens. I formulate the null hypthesis that all natural trees are green. I conduct the test that the red tree is artificial, and voila the hypothesis can only be rejected at the 1 per mill significance level.
Here we observe a small trend and use *model* trends to construct the distribution under the null-hypothesis. This model trends are independent from the observed value.
Pekka has a point when he says that we may have cherry picked one observation, and in purity one should compare two distributions.
This why I wrote that there are more issued in this comparison, and my explanation before was an illustration of how the test is conducted. Other issues is that it is known what are the statistical properties of the model trends. Are they independent ? do they sample the 'model space' randomly ?
@ Georg
'Von 88 bis 98 (vielleicht kann man das Intervall noch optimieren) war die Erwaermung sehr stark. Kannst du leicht ausrechnen, was die Wahrscheinlichkeit ist, dass diese starke Erwaermung noch innerhalb der Modelbandbreite bei ausschliesslichem GHG Forcing liegt?'
Very probably, the ensemble of trends forced without GHG would not contain the observed trend in that period, and the conclusion would be similar:
either the internal model variability is too small
there is an additional forcing.
We would had then detected a signal.
As in the present situation, we would be then confronted by the problem of attribution of the strong warming trends in that period. As with any other scientific theory , the attribution step cannot be proven. Theories can only be falsified, not proven. This point seem to be always difficult to understand for the non-scientist.
This essentially distinguish the efforts of main stream climatologist and sceptics. Whereas the task of the former is from the logical point of view much more difficult, actually impossible (to attribute the warming to GHG), the tasks of the sceptics is much easier, as they only have to find errors in climate models.
In other words, to find that a hypothesis is wrong in some aspect (to find a signal) is much easier than to assure that a hypothesis is completely correct.
Eduardo,
I don't mention cherry picking, and that's not exactly what I have in mind. Using the most recent data is an unique way of choosing what data to use, and that speaks against cherry picking. The problem is related to that, but the picking is in the space of all possible tests, not in the space of subsets of data.
When observed data is used in the choice of the test, the significance of the resulting numbers changes, and it changes in a way that may be extremely difficult to compensate for.
Observing that there's an unusually long period of very little rise is evidence against models that produce such periods very infrequently, but the inference is weaker than for a similar test performed on data unknown at the moment the test was chosen. The difficult question is: How much weaker the inference is?
@Pekka
"Using the most recent data is an unique way of choosing what data to use, and that speaks against cherry picking."
But the starting point is picked.
@ Pekka,
I agree with you that the 'test' is not completely clean.
In you read my post again, you will notice that I did not use the word 'significance' and refer mostly to the number of model trends that lie beyond an observed value.
The length of the interval , 15, 16 years, may be also subject to cherry picking.
In general, this goal of this comparison is descriptive, and it seems quite clear that model trends trends to be large compared to the recent observations.
@EDu
"die extern, von GHG,angetrieben simulierten Temperaturtrends falsch sind
-dass die von den Modellen erzeugte interne Variabilität zu klein ist
- außer GHG gibt es andere Forcings"
"falsche Trends" (Fall 1) hiesse ja im ersten Fall (rezente Trends) zu gross und im zweiten Fall (88-98) zu klein. Aus der Kombination (einerseits zu grosz andererseit zu kleine Trends) der beiden, koennte man dann nicht diese Moeglichkeit ausschlieszen?
@ georg
ich denke nicht. koennte es nicht so sein, dass in beiden Faellen die interne Modellvariabilitaet zu klein ist (war) und die geforceten Trends in der Mitte zwischen 88-98 und 98-2012 liegen ?
@ Georg,
When we are testing based on period that extends to the end of available data, choosing the starting point can be considered as part of the selection of the method. One possible test is also looking at the length of the period the temperatures have stayed in a given range where the starting point is thus an open variable.
Emphasizing the starting point would exaggerate its importance in comparison with other choices made.
Eduardo,
Enverstanden, weil the Mexihat hat-paradox findet hier keine Anwendung.
Don't agree. You picked 1998-2012 because your experience with model results led you to the assumption that this trend is rare. So in formulating H0 you used the same data from which you constructed the distribution under H0.
You implicitly acknowledge this in your answer to Georg, i.e. that testing the same H0 against the alternative of, loosely speaking, "real climate exhibits stronger trends than modelled climate" (with a suitably picked strong trend from observed time-series), likely would also result in the rejection of H0.
You conclusion from this (#14) is that "the modelled internal [decadal] variability is too small".
What about calculating the variance of the linearly de-trended period from 1975 to 1997? Would it be possible that this statistic from obs is unusually small compared to the respective distribution from simulations?
Also: If you want to frame this study as a hypothesis test, you should be able to precisely define a random variable as outcome of a random experiment, and a test statistic. Can you?
I think this study is a valuable explorative analysis to give hints where to continue real research. But I think stating the result as "... hypothesis rejected at the x% level" is misleading.
@ hvv
'You picked 1998-2012 because your experience with model results led you to the assumption that this trend is rare.'
The fact that two manuscripts were submitted at the same time to quantify how rare these trend is reflects that fact that it was not previously know how rare. The Mexican hat paradox would apply if I had first scanned the distribution of model trends and the selected one 15-year period in one of the simulations to claim that that particular model and that decade were somehow special. In other words, I select one of the realization of the distribution of the null-hypothesis, and this I am sure of the outcome of the test before conducting it. Here, the observed trends are not used to construct the distribution and although the observed trend seem small against the expected mean trend, there was no real feeling about the spread of the model trends, which is basically the result of the Fyfe, Guillet and Zwiers paper.
The HO proposed by Georg is different from what you have written. He proposed that the observed. trend in 80-98 is equal to the modelled trend without GHG forcing, and that distribution of trends could not be known without doing the simulations.
'I think this study is a valuable explorative analysis to give hints where to continue real research.
But I think stating the result as "... hypothesis rejected at the x% level" is misleading.'
And we didnt, if i recall properly. In our manuscript.
It is also not known which underlying distribution the model trends represented. So there are still open questions. On the other hand, one could argue that climate change is claimed to have been detected by basically the same machinery. Actually even more flagrant, because the warming observed in the 30s also lied beyond the CMIP3 model spread, and that time the explanation was a deficient simulation of internal variability.
'What about calculating the variance of the linearly de-trended period from 1975 to 1997? Would it be possible that this statistic from obs is unusually small compared to the respective distribution from simulations?'
The problem is here is that we need the spread of 15-year trends in a stationary climate. There is no direct way to estimate this from observations, without knowing what the forced variability is.
Let us reframe the problem in the following way.
If the temperature trend in the next 100 years is zero, all of us would agree that there is something seriously wrong with climate models. We would all agree if this happens for the next 50 years. 25 years ? 20 years?
This type of analysis addresses this question. It illustrates how long should a stagnation period be to be indicative that climate models, either their sensitivity or their internal variability, is not correct. So far, the analysis says that 16 years is not enough, but that 20 years will be a clear sign.
One factor that should affect conclusions is that we do actually know that the models cannot describe correctly the internal variability. Thus they may have the right amount of variability by accident, and they may have the right amount of autocorrelation in the variability by a much larger accident. But we should not be surprised at all, if they don't have the right amount of total variability or autocorrelations.
Knowing that the variability is likely to be in error makes in even more difficult to draw any conclusions on the climate sensitivity (TCR).
@ Eduardo,
This is somewhat OT but has the increase of GHG forcing any bearing on this?
CO2 was about 370 ppm in 1997 and now it is 400 ppm. The rise in the past 100 years has been about 100 ppm.
After having noticed that SOMEONE is reading our (Zwiers and me) opus on stats published at Cambridge, and is aware of the Mexican Hat, I feel an urge to comment. The concept has been first discussed in a book chapter from 1993, which is online available.
To some extent the examination of the recent 15- and 16 years trends is Mexican-Hat'ish. as the analysis was done after people had noticed a somewhat surprising slow warming in recent years.
This is a phenomenon very common in climate science, which is related to the inability to generate any new and independent data for testing hypotheses in a few years; even if we would wait now for ten years, we would possibly not have truly independent data, given the long memory in the system. We have seen similar things, when links are constructed between late fall sea ice deficits and harsh winter conditions in Europe, for example. Also the original detection studies, in the mid 1990s, were based on the knowledge that it is getting quickly warmer - a posteriori the motivation is used: we suspected a mechanism, and this suspicion is independent of the recent data.
It may be a worthwhile exercise to examine, why the thesis of an accelerated aerosol-driven development towards ice age conditions (see Rasool and Schneider, 1971) was abandoned and replaced by the GHG-thesis. Was this for reasons of better a-priori understanding or of a-posteriori actual development?
I guess - but do not know - the latter.
-Second comment follows-
Tamino edwards has a different take on this, asking the question:
"Riddle me this: if we had been told by an unimpeachable source on January 1st, 1998 that there would be no statistically significant temperature increase over the period from the beginning of 1998 through the end of 2013, what would we have predicted? How would that compare to what has actually happened?"
The short answer is: it was going to be much hotter.
Read here for the long answer:
http://tamino.wordpress.com/2014/01/30/global-temperature-the-post-1998-surprise/
My second comment - what we did was a counting exercise, not a determination or probabilities. This counting exercise formally looks like a statistical test of a null hypothesis with a predefined significance level, but it is not.
First,the important basic assumption "Let X be a random variable" is violated. We can not define a population of all valid scenarios, we can deal with a "given set of scenarios", which is a more or less arbitrarily assembled set of available simulations.
See: von Storch, H. and F.W. Zwiers, 2013: Testing ensembles of climate change scenarios for"statistical significance" Climatic Change 117: 1-9 DOI: 10.1007/s10584-012-0551-0
We are describing the range of possibilities without any uncertainty, as the set of simulations is completely known. We can, howver, nbot say, how the range would change if we add another 100 scenarios. Plausibly, it would not change much, but if models with significantly revised parameterizations may return other trends, we do not know. Thus, we do not do a statistical test and conclude with a statement a bout the probability of error.
Instead we say: e.g., 2% of all trends in the set of available scenarios (which are selected according to ac criterion of almost linear GHG concentration increase) are smaller than one derived from 1998-2013.
If someone considers this an alarming finding or not, is left to everybody's judgment.
Obviously, the longer the phenomenon continues after we (or others in 2009) noticed the slow warming, the less Mexican Hat'ish the problem becomes.
In short - even if the procedure looks like a statistical assessment, it is not; it is an empirical plausibility argument.
The trend in HadCRUT4 for the period 1984-1998 was 0.26 K/decade, which corresponds to the 64% percentile of the simulated trend ensemble as calculated here (2005-2006, scenario RCP4.5) Thus, the observed trend was a bit higher than the median value, which is 0.23 K/decade.
The 95% percentile is 0.41 K/decade; the 5% percentile, 0.08 K/decade
@Edu
"ich denke nicht. koennte es nicht so sein, dass in beiden Faellen die interne Modellvariabilitaet zu klein ist (war) und die geforceten Trends in der Mitte zwischen 88-98 und 98-2012 liegen ?"
Das meinte ich. Wenn einmal zu hoch und einmal zu niedrig, dann koennte es eine Problem mit der Variabilitaet sein.
@Pekka
I dont understand your answer. Even if for a reason I dont yet understand the end of the observed data serie is a "natural" point the fact of loocking 10,15 or 20 years back is picked- cherry or not.
More on this in Nature by J. Curry
@Edu
From the very friendly and positive Nature opnion peace of Judith
"Laudably, Cowtan and Way have made their data and computer code available following publication of their paper "
and
"Cowtan and Way4 present an alternative way of handling regional gaps in the surface temperature record, and conclude that the slower warming over the past 15 years or so has not been as significant as thought."
on one side
and from the rather harsh an negative evaluation of the paper from the website of Mrs Curry
"So I don’t think Cowtan and Wray’s analysis adds anything to our understanding of the global surface temperature field and the ‘pause.’"
So it does not add anything at all to our knowledge but I write an article about it how much I like it.
Funny.
An argument could be also made here that the focus on the Arctic is also a kind of cherry-picking, since we a priori know that Arctic temperatures have risen faster. Why not focus on Africa and try to fill the data gaps there ?
Independently of the Arctic, however, there is still a 'remarkable' difference between models and observations (let us formulate it in that way). Fyfe, Gillet and Zwiers did mask the model data according to the availability of the HadCRUT4 observations and they still find that the observed HadCRUT4 trend is at the fringe of the model ensemble.
I think that a more constructive stance is to ask ourselves what are the model missing, and why their internal variability seem to be small
Eduardo, you may benefit from reading this:
https://skepticalscience.com/global-warming-since-1997-more-than-twice-as-fast.html
The Figure answers your question about Africa.
For those who wonder: Cowtan and Way actually did what Eduardo wonders about them not doing: they looked at coverage bias in Africa, too. In fact, they did so for the whole globe, applying their method to get essentially full coverage.
Bam
@Georg Hoffman
Perhaps Curry changed her mind. Cowtan and Way did an outstanding job of engaging with skeptics both at Curry's blog and at climateaudit. I came away with the impression that their work was pretty good, and I think others there were impressed as well. Not saying the work is right, but they did well in defending it.
@Pekka, others: granting that strict hypothesis testing may not be appropriate, one would think that common sense would be. These models were finalized around the start period of this time period. Since that time, they have one and all drifted hot, pretty much together, pretty much all runs, pretty much consistently. There are essentially no models left that are doing a good job.
It would be nice if you all could make this statistically precise, but I would think that any rational person ought to conclude that we need new models, and that these models should not be used for overall surface temperature prediction.
If someone would verify that the out-of-sample error is much bigger than the in-sample error (before the models were fixed), a rational person should conclude as well that the models were tuned/curve-fitted whether the modelers think so or not. I don't know what the fix for that would have to be.
I start by noting that what I had in mind when I wrote my above comments is close to what von Storch wrote in #21 and #23.
@Georg #25
Yes, fixing the starting point may involve cherry picking, but that's noise in the basic near impossibility of avoiding more severe cherry picking when the data is already known.
Furthermore there are perfectly valid tests for determining whether a period defined by some conditions is exceptionally long with predefined statistical confidence, assuming that other conditions of testability are satisfied (they are not in this case).
This is a very common dilemma in all fields where most data is historical and new data accrues too slowly. The fundamental dilemma is that tests are unavoidably formulated (to mention just two issues)
- Knowing that nothing more dramatic has occurred than actually has. This is in many cases a very essential source of bias, because exceptionally strong phenomena may have a large influence in spite of their rareness.
- Tests are typically developed to get a maximally clear indicator for the small likelihood of what appears exceptional in the data. Because the number of different possible "black swans" is very large, one of the many is much more likely to occur than any specific one. When the likelihood of only that one that has really occurred is considered, severely wrong conclusions may be drawn.
There are many other reasons that make it very difficult or virtually impossible to judge, when an observation is really significant, and when not.
At some point a longer and longer hiatus starts to be really significant, but what's that point?
@ Bam,
you may also benefit from reading the original article, instead of secondary sources.
'The Arctic is likewise the primary source of
uncertainty in this work. Further work is needed to address the differing behaviour of the land and ocean domains.'
Actually, two methods of interpolation have been applied. Only the results of the hybrid method are included in the paper, the method that 'should work better over ice'.
If I did not overlook it, no trend correction is given by the simple kriging method, unless it is in the supplementary material, which I have not read.
So, this paper targeted the Arctic specifically, and also used, in the hybrid method, the satellite data from UAH, not from RSS. Looking at my last figure in the post, one may wonder why.. The authors argue that the RSS data have poor properties at high latitudes. But one may also wonder that if they had used the RSS data over the tropics, their correction to the HadCRUt trend could have been even negative.
Yes, Eduardo, they spent most of their efforts on the Arctic due to the issues with land-ocean-ice. But they also did an infill for Africa, and you definitely suggested they did not.
Also, the argument for using UAH rather than RSS is that the latter excludes the high latitudes (that is, no coverage at all). The people at RSS have a good reason to ignore that data, and the problem is likely also present in the UAH data, but that is why they spend so much time on that hybrid approach. Note that Cowtan and Way thus do _not_ argue that they use UAH because RSS has poor properties at high latitudes.
Your last figure just shows what Cowtan and Way show: leaving out the arctic (and large parts of antarctic) has a major downward effect on the trend. RSS actually has a larger trend in the tropics than UAH, so your suggestion is highly unlikely.
A final note: my "secondary source" is the first author of the paper showing what they have done.
Eduardo,
thanks for the extensive answer (#17).
"Mexican Hat-ness" is not properly defined and it is a mess, that in these types of statistics, the a priory knowledge and even the intention of the researcher plays a role, which is not considered in the formalism. In this case I seem not to be alone with my perception.
A stronger statement: You have a number of n time-series from the same, "real" climate (X_(1..n)), draw one (X_1, "observations"), select and extreme 15-y trend (T_ext) from X_1 (that can be max(trend), min(trend), min(abs(trend)), whatever), and calculate the fraction (f) of the trends in all X_(2..n), "perfect model simulations" that are more extreme than T_ext. That would be about your method here in the "H0 is true"-case.
If f is smaller than, say 0.05, you somehow take that as an indication, painstakingly avoiding terminology from statistical testing though, that the ensemble of models (in this case an initialization ensemble of the perfect model) does not represent real climate. But in fact it does.
It is straightforward to show that you'd come to the wrong conclusion here much more often than acceptable if you want your method to be meaningful.
The HO proposed by Georg is different from what you have written...
The rest of the conversation makes perfect sense with my understanding of what Georg proposed. Must be some mis-understanding.
[But I think stating the result as "... hypothesis rejected at the x% level" is misleading.]
And we didnt, if i recall properly. In our manuscript.
You kind of didn't, right. But you kind of suggest, by leaving out how else this result should be interpreted, that it is still to be understood as some sort of, maybe not totally correct, but still strongly indicative, test. And your post #2, to which I was referring, clearly shows that this is how you think about it.
[Variance of linearly de-trended period]
There is no direct way to estimate this from observations, without knowing what the forced variability is.
I guess I agree.
@ 35
I am not sure whether I understood your paragraph properly. Do you mean to select an extreme observation from a sample and use that very same sample to construct the distribution of the HO ? If this is what you mean, of course this is the Mexican-hat paradox. It is , however, not the calculation presented here.
The distribution is constructed from the CMIP5 models. These data have been recently made available and are independent of the observe dtrend (no tuning...).
In the Mexican paraddox one can tell the results of test *exactly* prior to conducting the test itself. in other words, it is an artefact. Here, no one could know the results before hand. One could guess, for instance from the CMIP3 models, but that would be a physically based guess, not a physical artifact. If. for instance, the internal variability of the CMIP5 models were larger than in the CMIP3 models, the results of the test would have been different. Or if calculating overlapping or non-overlapping trends.
I agree that the cherry-picking caveat may apply, but not the Mexican-hat paradox, as I understand it.
Imagine that we are in 2100 and the trend has been zero. You could formally argue that the Mexican-hat paradox apply as well, and the calculation is not valid. This would be paradox in itself. The calculation cannot be formally valid depending in the length of the period: invalid if 15 years, valid if 100 years.
'The HO proposed by Georg is different from what you have written...'
Do you mean my comment 24 ?
yes, it is different. That comment is not supposed to be an answer to Georg and it is not tagged as such. It is just general information.
And your post #2, to which I was referring, clearly shows that this is how you think about it.'
'
In comment 2 I was trying to explain to Andreas the basic reasoning, as he seemed to be confused. The calculation is not formally a test for more fundamental reasons than cherry pecking, namely we do not know what the model ensemble represents in a 'model space'
But indeed I think that the calculation is strongly indicative that something important is missing in the models, as I explained: either another forcing, or internal variability or sensitivity. From my informal contacts in the last months, I am not alone here.
Eduardo
I am not sure whether I understood your paragraph properly. Do you mean to select an extreme observation from a sample and use that very same sample to construct the distribution of the HO ?
No, that is not what I meant. I argue that even without the "Mexican hat"-fallacy the method is not terribly meaningful.
1. You look at an observed time-series and select an extreme trend.
2. Then you calculate the fraction of trends that are more extreme than the one from step 1 from a freshly obtained set of time-series. Assume that the freshly obtained set of time series is from the same population than the observed one, e.g. being the result of an ensemble model simulation with "the perfect climate model".
3. Find that this fraction is below 0.05 quite often and that consequently it is quite likely for you to conclude that that "perfect model" is imperfect.
You can check this easily by simulating a synthetic climate, say as
an AR(1) process, phi=0.2, sigma=0.1 K, with trend 0.02 K/y.
That is a poor replacement for real climate, but if my claim holds, then the onus is on you to show that it doesn't hold for real climate.
In comment 2 I was trying to explain to Andreas the basic reasoning, as he seemed to be confused.
His confusion seemed to stem from the very issues we were discussing in the following, not from failure to get the basic idea of a statistical test.
The calculation is not formally a test for more fundamental reasons than cherry pecking, namely we do not know what the model ensemble represents in a 'model space'
I can live with what you consider "a more fundamental problem", precisely because it is unavoidable if you deal with questions like that. Also soft knowledge and general expertise can serve to bracket the error introduced and results might still remain indicative of something.
The other problem, which I focus on, only shows up if you limit yourself to a particular 15-year trend to obtain information about whether and how climate models are wrong.
I believe too that "something important is missing in the models". Particularly with respect to the representation of decadal variability. I am afraid that your calculation doesn't contribute to that belief (but only after thinking about it a bit more, inspired by your comment :).
Your comment #18. "How long has the low trend to continue until we have some evidence that the models are wrong in a related way?"
I'd argue that if your analysis says "20 years" then we have to wait 20 years from now on to conduct the test.
Reiner #22
Thanks for the link to Tamino's article. Note that he is addressing a quite different question than Zorita/von Storch. He asks whether the post-1998 record is consistent with the hypothesis that global warming continues unabated in the way it was observed between the seventies and 1998. In other words he is taking a cheap shot at the "sceptics" who claim that there would be evidence that global warming has stopped.
His analysis is straight forward and clear-cut and the answer is "yes". While he was also inspired by the public attention to the "hiatus", his question is not scientifically interesting - anybody who has looked at temperature plots long enough comes to the same conclusion by unaided eye inspection. He is doing public education. This is in contrast to Zorita/von Storch, who address an important and topical question.
Rainer, are you sure? From taminos comment: "That kind of cherry-picking requires a large compensation to statistical analysis, one which makes it clear that there’s no justification for a massive research project to investigate the post-1998 blazing heat. It also makes clear that there’s no justification for running off at the mouth about the so-called “pause.”
Is he right? He made a "strait foreward" analyse and took the trend 1975...1997 and stretched it, anyway...in his post one never reads something about the slope: it's 0,12K/ decade (GISS). Quite low, isn't it? Take another approach: Stretch the trend from 1987 to 2005 ( also a 19 years long interval...) to both ends- to 1979 on the one and to 2013 on the other. The slope is 0.2 K/decade...and voila: The temperature data from 2011 on are well below sigma of the trend 1987...2005. What have I done? I cherry picked an interval for the trend calculation, it has the same length as this of tamino. The slope of the trend is in the region of the IPCC- forecasts (0.2 deg/decade) and the same did tamino, never mentioned his quite low trend slope. What could be a proper approach: a 9 year lowpass...and the pause is clearlxy visible. See http://www.dh7fb.de/nao/taminocherry.gif .
The trend 0.12 C/decade agrees perfectly with the average warming since 1950 that AR5 indicates as equal to the most likely rate of anthropogenic influence. It does not agree as well with most climate models.
Indeed, see the trend slopes of climate models: http://climateaudit.files.wordpress.com/2013/12/fig-1-tcr-post-cmip5-79-13-temp-trends_ca24sep13.png?w=720&h=480 .
( the figure was made by Nic Lewis). No one must wonder that the data match very well a "below model trend" and so the message684953 28 of taminos post is: The trend slopes of the models are too high. If it was his intention? ;-)
@ hvw
Danke (s. #37). Sie haben mich sofort verstanden, können es aber viel präziser formulieren.
@ Eduardo
Mir scheint, Sie reagieren teilweise etwas dünnhäutig. Warum? Ich freue mich, dass ich hier einer hochinteressanten, konstruktiven Diskussion beiwohnen konnte. Die Art und Weise, wie hier diskutiert wurde, hatte für mich etwas von "science at its best".
Mit "dünnhäutig" meine ich z.B., dass Sie "cherry picking" ansprachen, so, als müssten Sie sich gegen diesen Vorwurf verteidigen (den niemand erhoben hat). Für mich beinhaltet "cherry picking" die Absicht, mit Tricks zu täuschen, daher habe ich nie diesen Begriff hier benutzt. Es ging doch nie um ihre Person oder gar ihre Integrität, sondern einzig um die Frage, ob man die Argumentation im Sinne eines Hypothesentests benutzen kann.
Danke,
Andreas
@ 37
hvv,
ok, I understand what you mean.
Sue, the possibility that the observed trend comes from the model distribution is always there, and we just had hit an an event that lies below the 2% percentile. This is why one should compare two samples, one from the models and one from observations, but unfortunately we do not have a sample large enough from observations.
This being said, however, the same argument could be made to the reasoning of the IPCC that Georg suggested above: the period 1980-1998 the model ensemble driven by natural forcings only had a lot of problems simulating the observed trend. perhaps it was a rare event , above the 999% percentile ? I do not see a logical difference between both situations. The IPCCc 'test' was also conducted a posteriori, yet it has been presented as a proof that the 1980-1998 trend is very likely anthropogenic.
'His confusion seemed to stem from the very issues we were discussing in the following, not from failure to get the basic idea of a statistical test.'
Then I should have explained in another way. It is difficult to know before hand though.
'I believe too that "something important is missing in the models". Particularly with respect to the representation of decadal variability. I am afraid that your calculation doesn't contribute to that belief '
Well, I think it does, but of course you are entitled to your opinion. I am not sure whether the spread of model trends for different time segments was that well known, although it is easy to calculate it. Actually, nobody seemed to be very much interested on that spread until the hiatus appeared.
If you believe that the decadal internal variability is misrepresented by the models, then you cannot believe in the 'detection of climate change' as this detection is based on estimations of internal variability from models. At least there is an unquantifiable uncertainty there.
@Andreas"
Sie schreiben:
"Mit "dünnhäutig" meine ich z.B., dass Sie "cherry picking" ansprachen, so, als müssten Sie sich gegen diesen Vorwurf verteidigen (den niemand erhoben hat). Für mich beinhaltet "cherry picking" die Absicht, mit Tricks zu täuschen, daher habe ich nie diesen Begriff hier benutzt. Es ging doch nie um ihre Person oder gar ihre Integrität, sondern einzig um die Frage, ob man die Argumentation im Sinne eines Hypothesentests benutzen kann."
Sorry im Voraus!
Aber, dies ist wohl ein schlechter Witz?!
Cherry-Picking?
Die letzten 15 Jahre? 30 Jahre? 115 Jahre? Nach allem was wir bösen zweifelnden Laien lesen mussten von seitens eines Georg H. z.B. oder eines Stefan R. und unzähliger Andreasse muss man sich schon sehr zurückhalten um nicht in schallendes Gelächter auszubrechen.
Solange der "hiatus" anhält ist es so wie Eduardo es hier erklärt. Das versteht sogar jedes Kind.
"Science at it's least" würde ich das nennen, lieber freundlicher Andreas, der ja eigentlich gar nichts sagen wollte.
Und der Spaß fängt ja gerade erst an. :-)
Yeph
"Nach allem was wir bösen zweifelnden Laien lesen mussten von seitens eines Georg H. z.B. oder eines Stefan R. und unzähliger Andreasse muss man sich schon sehr zurückhalten um nicht in schallendes Gelächter auszubrechen."
Hallo Yeph,
z.B. worüber?
MfG
S.Hader
hvw
Sure, the aim was different. And I had a different author in mind, Tamsin (not Tamino --sorry if you read this!). She has an interesting blog:
http://blogs.plos.org/models/
Eduardo, #43
ok, I understand what you mean.
Thanks!
The IPCCc 'test' was also conducted a posteriori, yet it has been presented as a proof that the 1980-1998 trend is very likely anthropogenic.
Yes, I would consider such an argument invalid. Are you sure the IPCC has put that forward?
...Well, I think it does, but of course you are entitled to your opinion
Sorry, that was a bit harsh. Let's put it like that: My perception about the value of this exercise dropped more than usual, between reading the abstract and really thinking it through. The abstract reads:
...we find that the continued warming stagnation over fifteen years, from 1998 -2012, is no longer consistent with model projections even at the 2% confidence level.
This language clearly implies a confidence interval and a hypothesis test. Yes, the caveats are duly mentioned in the "Supplementary text", but no interpretation is given how this violation of the "fundamental sampling assumption" should be interpreted. The reader will think "Ok, some practically not relevant assumption violated, happens, I remember the 2% probability though, what else?
Good that Hans von Storch was quoted far and wide, directly and indirectly, saying: "A trend, which we believe happens rarely in real climate, but really have no clue, showed up in our climate simulations only rarely".
Oh, wait.
Actually he said something entirely different, but equally correct.
If there was no politicisation of climate science, no "skeptics" induced media attention to the "hiatus", you would have done that calculation, no question. But would you have written it up so nicely, submitted it to Nature, written blog-posts and updates about the impact of one more datapoint? I guess not. This exercise has been oversold.
Continued ...
Part 2
If you believe that the decadal internal variability is misrepresented by the models, then you cannot believe in the 'detection of climate change'
Good point. I did not say "misrepresented". What I mean is that to my knowledge the physical processes relevant for decadal variability are not well understood and that we still suck at even scratching the potential predictability. Correct me if I am wrong, this field seems moving fast now. I have good reasons to believe that detection studies such as optimal fingerprinting are meaningful and deliver robust results anyways. These reasons are 1) that other sources than model simulations contain information about internal variability (paleorecords, obsdata) that help to constrain estimates of its magnitude, their problems (time-resolution, ext. forcing, short records ..) notwithstanding. Much more importantly is 2) that the sensibility of attributions studies to estimates of nat. variability can be and has been examined and the results reinforce the validity of the attribution studies.
All this I believe as I can't possibly read, understand and evaluate (let alone reproduce) the science involved. I believe this, because my little personal experience supports the idea that the huge bulk of researchers have an attitude as demanded by this tradition called "science", which results in, broadly speaking, me trusting other people's write-up. Hans von Storch calls for vigilance against letting politics (or other forces) taint scientific work and/or presentation because science might loose the trust of the public and become "un-sustainable". I'd like to state that much more dangerous, really existential and the quickest way to irrelevance for science is not the loss of some authority granted by the general public, but rather the loss of trust of the researchers themselves into the functioning of their own tradition and into a majority of peers that shares an attitude and the ethics which will let the good stuff float atop, in due course.
An excellent starting point to start practicing this vigilance is the interpretation of statistical results, in particular when the epistemological power of hypothesis tests, as applied to controlled experiments, is falsely ascribed to the statistical analysis of observational studies.
Post a Comment (pop-up window,non-moderated)